Current Research
I’m interested in dark-anything, Type Ia supernovae and the Hubble constant.
Weak lensing of Type Ia Supernovae
I’ve been looking at what weak lensing can tell us about dark matter.
In weak lensing, the gravitational potential well of the dark matter halo surrounding a galaxy or cluster bends light and changes the shape of a background image (known as shear) in exactly the same way a lens does. Images are also magnified (or de-magnified if they pass through voids). However since we don’t know how luminous the background galaxy would have been without the lens (and the effect is very small), it’s hard to make use of this.
However, we do know the luminosities of Type Ia supernovae to within about 0.1 magnitudes. They are also bright enough to be seen at distances where lensing could have a measurable effect. Nevertheless, although the Pantheon sample comprises 1,048 SN Ia, detecting lensing remains challenging as for a typical SN Ia the magnification may only be -0.04 to 0.02 magnitudes.
Detecting weak lensing magnification
We propose a model for the amount of weak lensing of a given SN Ia. Our model has two free parameters : the mass-to-light ratio of foreground dark matter haloes compared to their associated galaxies, and the radial slope of their density profile.
Using the Pantheon catalog in combination with photometric galaxy data from SDSS, we find this estimator correlates with the residuals of the SN Ia to a Hubble diagram fit at a significance of 3.6\(\sigma\). This is the most robust detection in the literature of the magnification of SN Ia luminosities.
Our model also allows us to derive Bayesian posteriors for the mass-to-light ratio and radial slope. We find that the NFW profile is consistent with the data, and the mass-to-light ratio suggests \(\sim 0.5\) of the dark matter in the Universe is bound to galactic haloes.

The estimated magnification of SN Ia in Pantheon is plotted on the x-axis, and their Hubble diagram residuals on the y-axis. The axes have been roughly normalised to units of standard deviation. The effect of lensing is seen as the grouping of points towards the top right and bottom left quadrants.
The scatter of weak lensing is found to be \(\sim 0.06\) magnitudes at redshift \(z=1\), and proportional to \(d^{3/2}\) where \(d\) is the comoving distance to the source.

The scatter in SN Ia magnitudes increases with distance.
Cosmology in an inhomogeneous universe
Cosmologists rely on model distance formulae derived under the assumption of homogeneity and isotropy. But we live in a clumpy universe : how can we be sure those formulae are valid?
We focus on the effect of weak lensing on cosmological parameter inference. This is not the full story as we do not allow for obscuration or strong lensing, but using our model estimator we can de-lens luminosity distances and recalculate cosmological parameters. We find that although Pantheon shows a bias towards over-dense lines of sight at moderate significance, this only lowers the matter density \(\Omega_m\) by 0.5%.
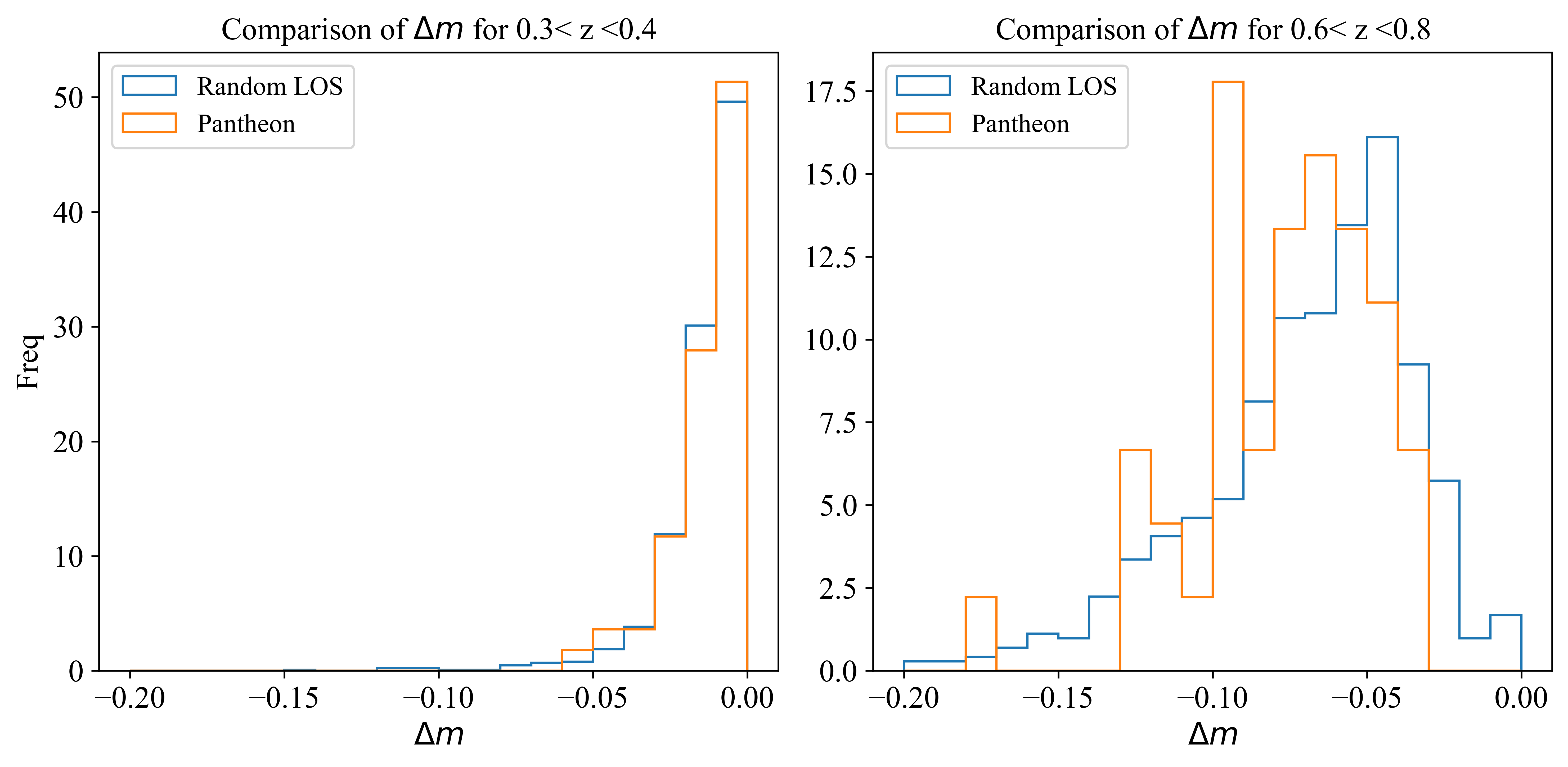
The lensing magnification of Pantheon SN Ia in a mid redshift bucket is consistent with a random line of sight, however a deeper bucket shows here Pantheon has a bias to over-dense lines of sight.
Papers
The weak lensing magnification of Type Ia supernovae P.Shah, P.Lemos and O. Lahav
Correcting Type Ia supernova luminosity distances for weak lensing In Prep, P.Shah, P.Lemos and O.Lahav
Hubble Constant
There are as many opinions on the Hubble constant as there are ways to calculate it! Two sets of results that are much discussed are from the SHOeS team (who use geometrical distances to calibrate Cepheid magnitudes, and Cepheids to calibrate Type Ia supernovae), and from the Planck team (who use the power spectrum of the CMB plus the assumption that the universe is \(\Lambda\)CDM). These two results tempt the explanation that it is an “early” vs “late” tension, and perhaps a solution can be found in modifying the expansion history away from \(\Lambda\)CDM with some novel physics. However, this is to discount local distances from TRGBs that are inconsistent with Cepheids (although there is some debate on the calibration), plus data from galaxy surveys which when combined with a density constraint from BBN is consistent with CMB results. Additionally, the Planck results have a peculiar internal inconsistency dubbed \(A_{\rm lens}\), although the significance of this is unclear.
Our review of this topic had three aims. Firstly, we aim to provide a pedagogical introduction to the results. Our paper should be accessible to undergraduates, while at the same time providing enough detail on systematics to satisfy the more experienced reader. Secondly, our aim was to provide an impartial (but perhaps imperfect!) opinion as to the historical and future development of most of the main probes of \(H_0\). Thirdly, for astronomers in a hurry, we make recommendations about what value to use.
A buyer’s guide to the Hubble constant P.Shah, P. Lemos and O. Lahav, A&A Review, Vol 29, Issue 1, Dec 2021
Continue with Publications

